El punto medio entre dos valores: El Teorema del Valor Medio

El Teorema del Valor Medio es un concepto fundamental en el cálculo diferencial que establece una relación entre la derivada de una función y su incremento promedio en un intervalo dado. Este teorema, también conocido como el Teorema de Rolle, fue formulado por primera vez por el matemático francés Michel Rolle en el siglo XVII.

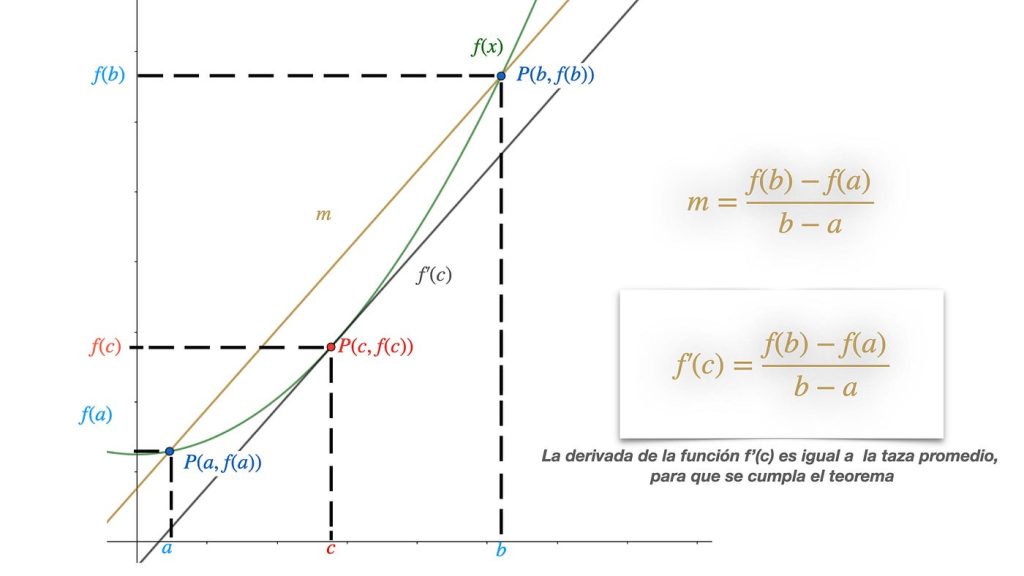
El Teorema del Valor Medio establece que si una función es continua en un intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual al incremento promedio de la función en el intervalo [a, b]. En otras palabras, existe un punto en el intervalo donde la pendiente de la recta tangente a la curva es igual a la pendiente de la recta secante que une los puntos (a, f(a)) y (b, f(b)).

Este teorema es de gran importancia en el cálculo diferencial, ya que permite establecer propiedades y relaciones entre las funciones y sus derivadas. Además, es utilizado en la demostración de otros teoremas y en la resolución de problemas relacionados con la optimización y el análisis de funciones.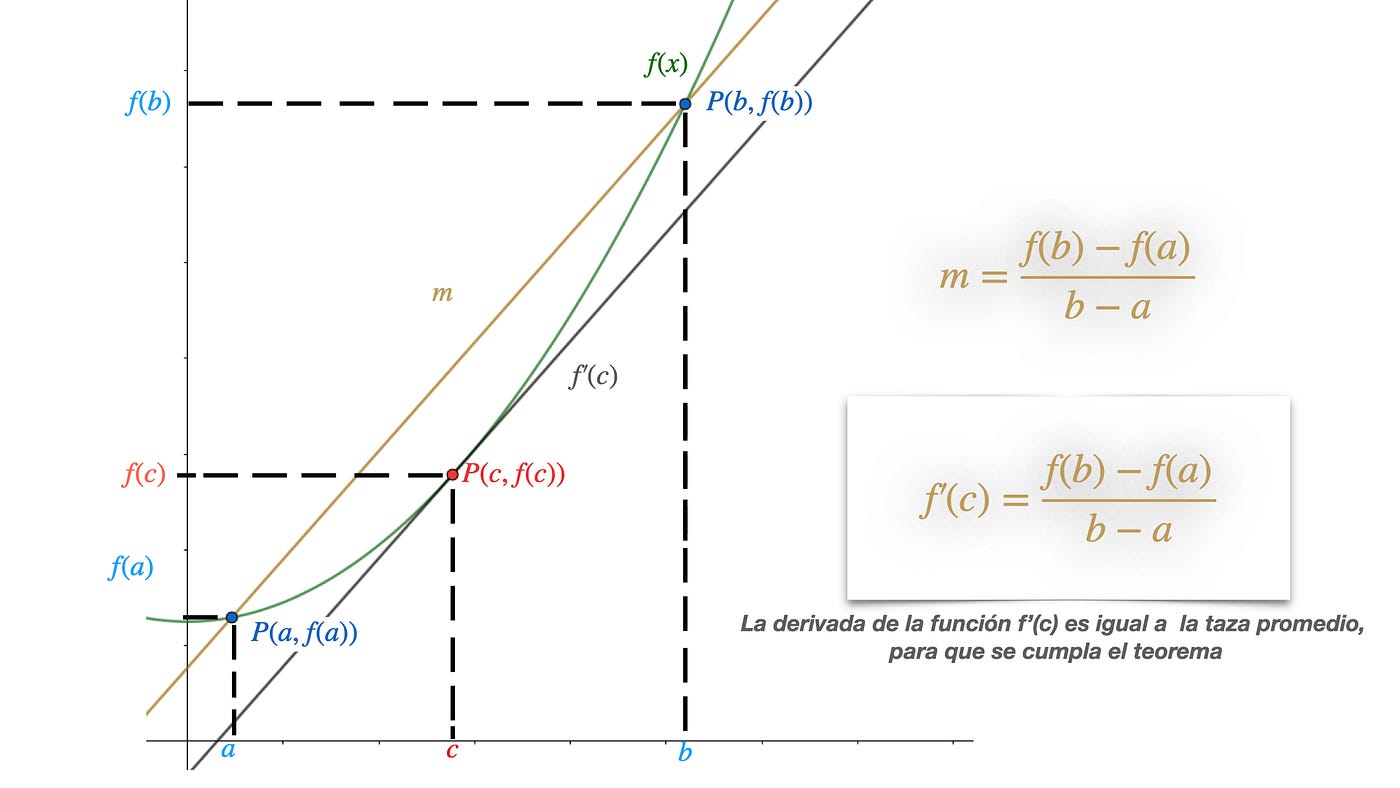

Teorema de Gauss

El Teorema de Gauss es un principio fundamental en el campo de la física y las matemáticas. Fue formulado por el matemático y físico alemán Carl Friedrich Gauss en el siglo XIX. Este teorema establece que el flujo eléctrico a través de una superficie cerrada es proporcional a la carga eléctrica encerrada por dicha superficie.

En términos más simples, el Teorema de Gauss nos dice que la cantidad de líneas de campo eléctrico que atraviesan una superficie cerrada es igual a la carga eléctrica total dentro de esa superficie dividida por la constante dieléctrica del medio en el que se encuentra.

Este teorema es de gran importancia en el estudio de la electrostática y tiene aplicaciones en diversos campos, como la física de partículas, la teoría electromagnética y la ingeniería eléctrica. Además, el Teorema de Gauss es una herramienta fundamental en el cálculo vectorial y se utiliza para resolver problemas de flujo y divergencia en ecuaciones diferenciales parciales.

Definición del Teorema del Valor Medio

El Teorema del Valor Medio es un concepto fundamental en el cálculo diferencial que establece una relación entre la derivada de una función y su incremento promedio en un intervalo dado. Este teorema establece que si una función es continua en un intervalo cerrado [a, b] y derivable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual al incremento promedio de la función en el intervalo [a, b].

En términos más simples, el Teorema del Valor Medio establece que si una función es continua y derivable en un intervalo, entonces en algún punto dentro de ese intervalo la pendiente de la recta tangente a la curva de la función será igual a la pendiente de la recta secante que une los puntos extremos del intervalo.

Aplicaciones del Teorema del Valor Medio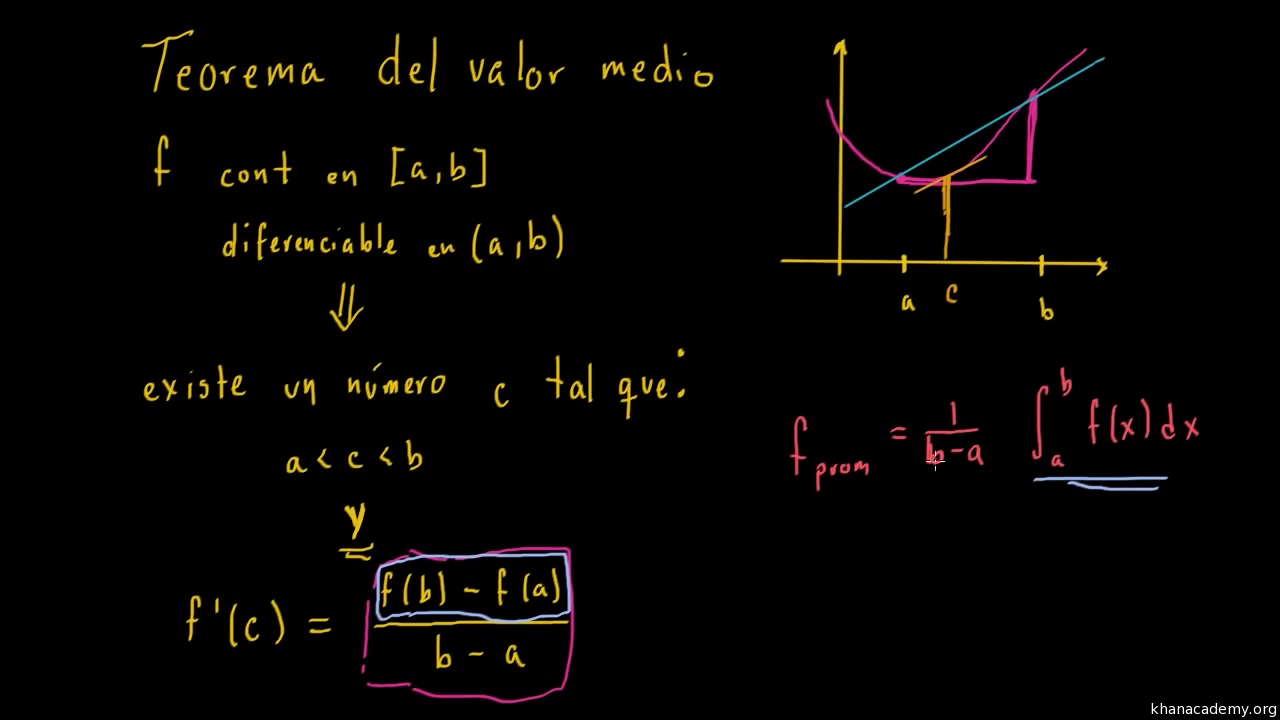

El Teorema del Valor Medio es una herramienta fundamental en el cálculo diferencial que tiene diversas aplicaciones en diferentes áreas de las matemáticas y la física. Una de las aplicaciones más comunes es en el estudio de las funciones y sus propiedades.

En el campo de la física, el Teorema del Valor Medio se utiliza para analizar el movimiento de objetos en una trayectoria determinada. Por ejemplo, si se conoce la posición de un objeto en diferentes momentos del tiempo, el teorema permite encontrar la velocidad media del objeto en ese intervalo de tiempo.

Otra aplicación importante del Teorema del Valor Medio es en el cálculo de integrales definidas. Este teorema establece que si una función es continua en un intervalo cerrado y diferenciable en el intervalo abierto, entonces existe al menos un punto en el intervalo donde la derivada de la función es igual a la pendiente de la recta secante que une los extremos del intervalo.

En resumen, el Teorema del Valor Medio es una herramienta poderosa que se utiliza en el análisis de funciones, el estudio del movimiento de objetos y el cálculo de integrales definidas. Su aplicación en diferentes áreas de las matemáticas y la física demuestra su importancia y utilidad en el estudio de fenómenos y propiedades.

Prueba del Teorema del Valor Medio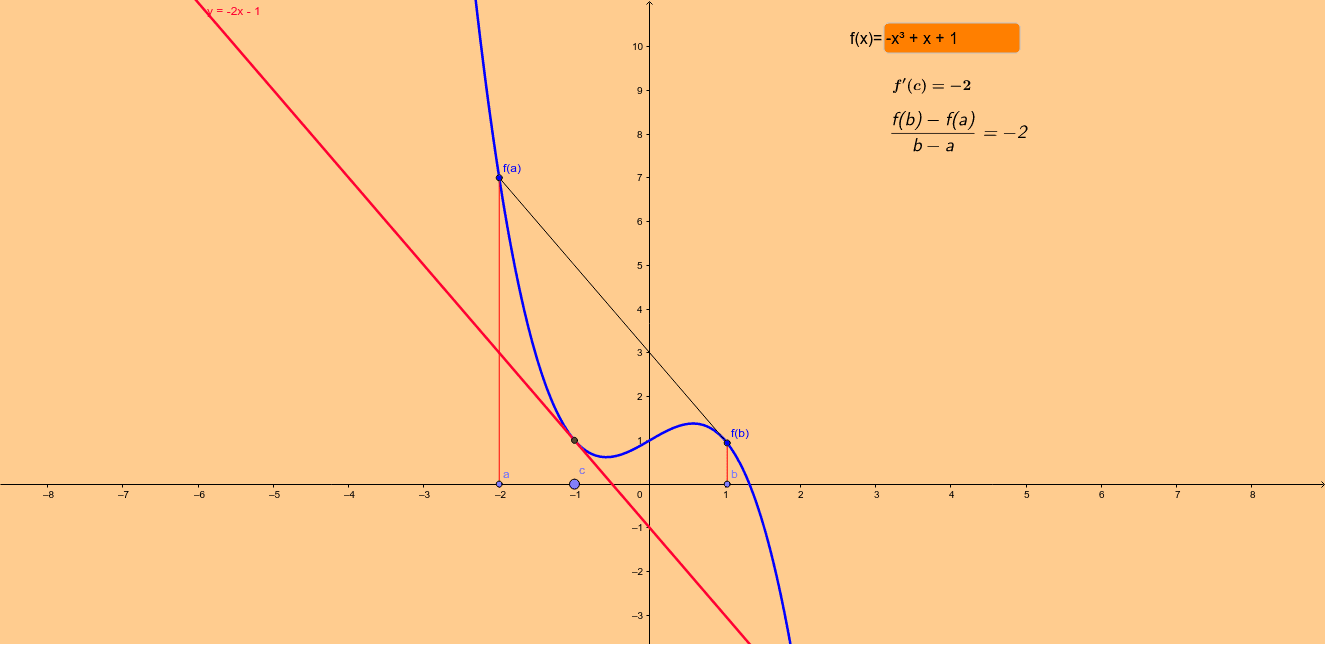

La prueba del Teorema del Valor Medio se basa en el concepto de derivada de una función. Supongamos que tenemos una función continua en un intervalo cerrado [a, b] y derivable en el intervalo abierto (a, b). Según el Teorema del Valor Medio, existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual a la pendiente de la recta secante que une los puntos (a, f(a)) y (b, f(b)).

Para demostrar esto, consideremos la función f(x) en el intervalo [a, b]. Si la función es constante en todo el intervalo, entonces su derivada es cero en todos los puntos y el Teorema del Valor Medio se cumple trivialmente. Si la función no es constante, entonces su derivada no es cero en algún punto del intervalo.

Supongamos que la derivada de la función en el punto c es diferente de cero. Esto implica que la función tiene una pendiente en ese punto. Ahora, consideremos la recta secante que une los puntos (a, f(a)) y (b, f(b)). La pendiente de esta recta secante es igual a la diferencia de las coordenadas y dividida por la diferencia de las abscisas, es decir, (f(b) – f(a))/(b – a).

Consecuencias del Teorema del Valor Medio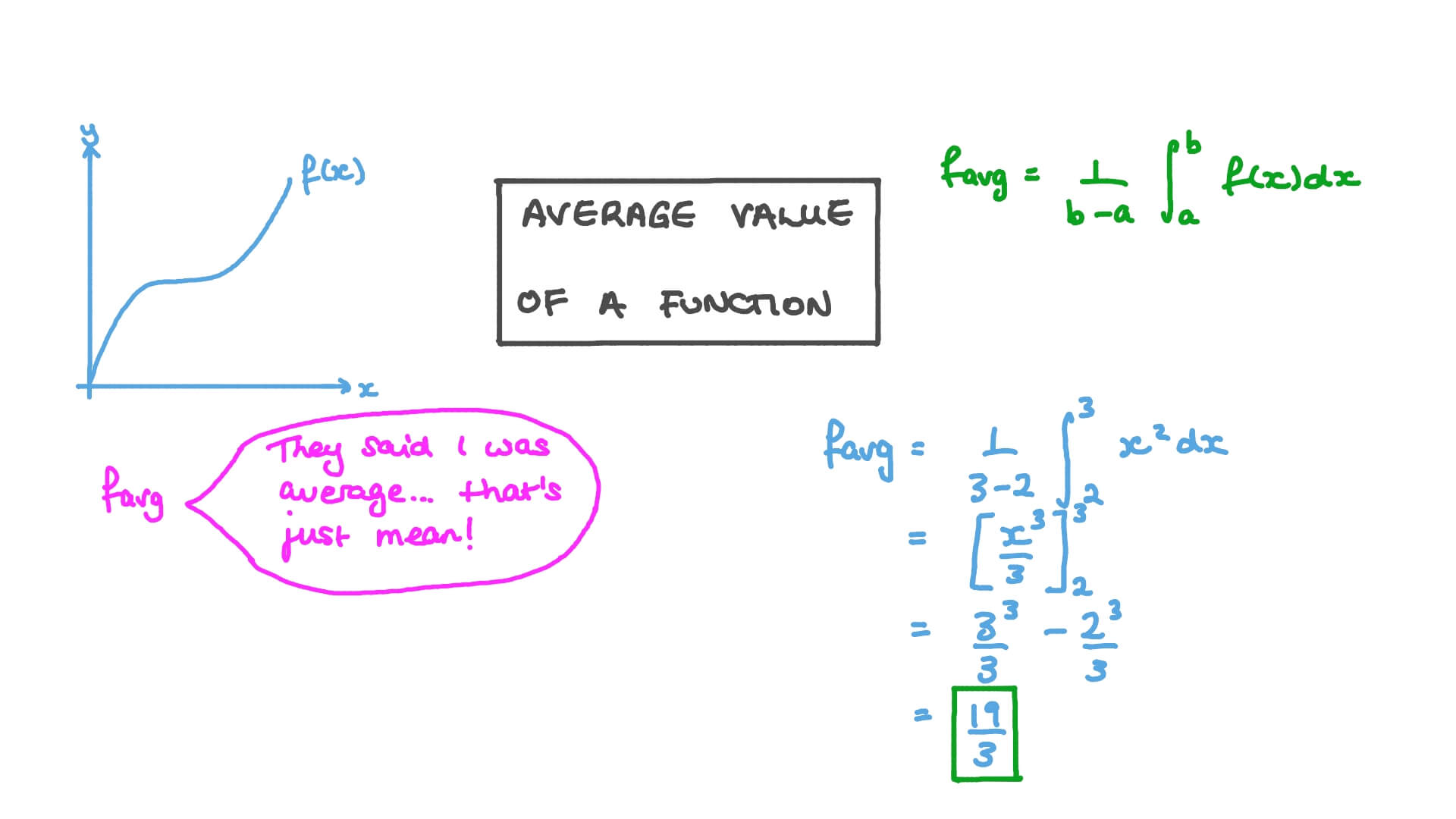

El Teorema del Valor Medio es una herramienta fundamental en el cálculo diferencial que establece una relación entre la derivada de una función y su incremento promedio en un intervalo. A partir de este teorema se pueden derivar varias consecuencias importantes.

Una de las principales consecuencias del Teorema del Valor Medio es la existencia de puntos críticos en una función. Si una función es continua en un intervalo cerrado y diferenciable en su interior, entonces existe al menos un punto en el intervalo donde la derivada se anula. Este punto se conoce como punto crítico y puede ser un máximo, mínimo o punto de inflexión de la función.

Otra consecuencia relevante es la posibilidad de determinar la concavidad de una función a partir de su segunda derivada. Si la segunda derivada es positiva en un intervalo, entonces la función es cóncava hacia arriba en ese intervalo. Por el contrario, si la segunda derivada es negativa, la función es cóncava hacia abajo. Estas propiedades son útiles para analizar el comportamiento de una función y determinar la existencia de puntos de inflexión.

En resumen, el Teorema del Valor Medio tiene importantes consecuencias en el análisis de funciones. Permite determinar la existencia de puntos críticos y establecer la concavidad de una función. Estas propiedades son fundamentales para comprender el comportamiento de una función y realizar cálculos más avanzados en el campo del cálculo diferencial.

Teorema del Valor Medio para Derivadas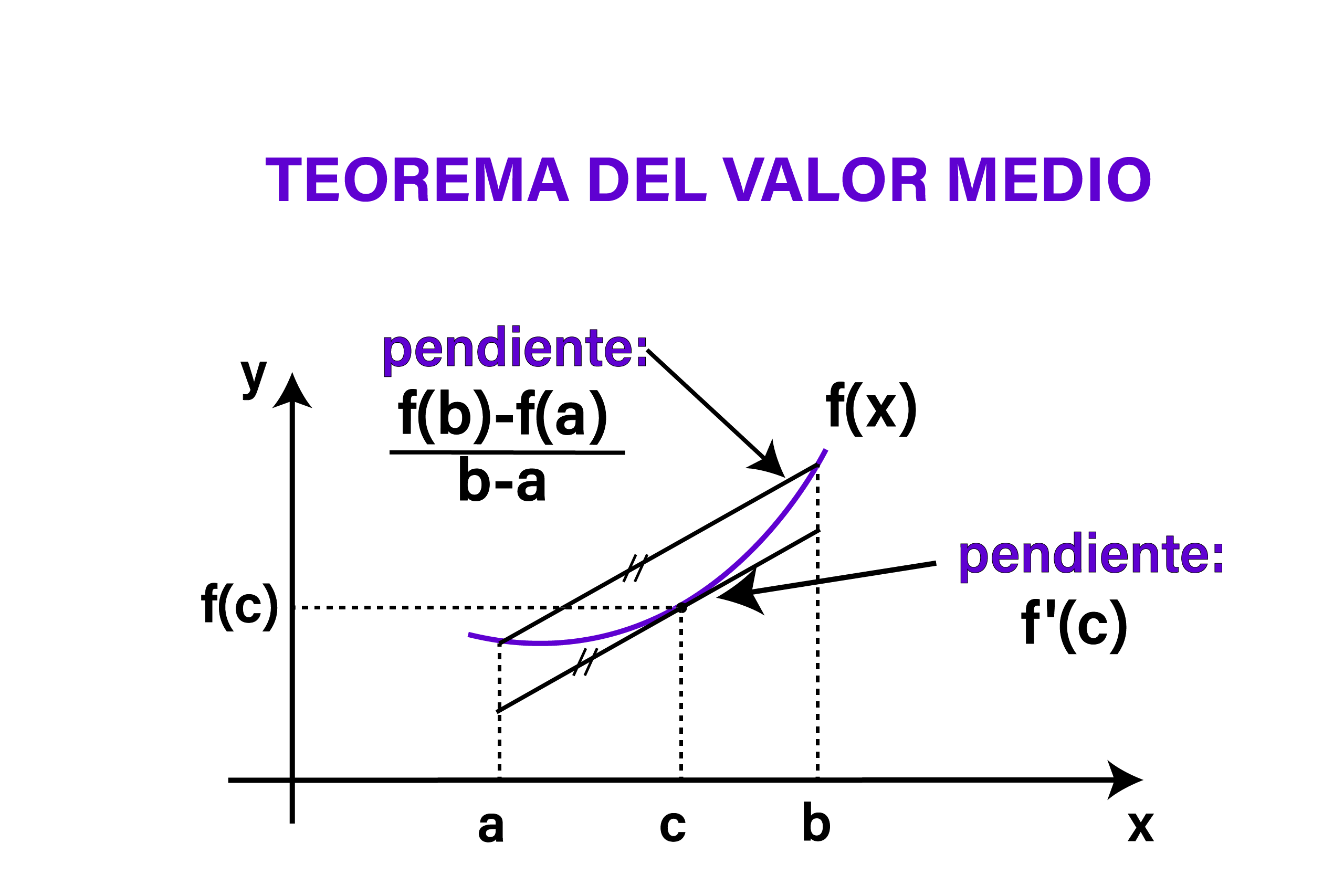

El Teorema del Valor Medio es un concepto fundamental en el cálculo diferencial que establece una relación entre la derivada de una función y su incremento promedio en un intervalo dado. Este teorema establece que si una función es continua en un intervalo cerrado [a, b] y derivable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual al incremento promedio de la función en el intervalo [a, b].

En términos más simples, el Teorema del Valor Medio nos dice que si una función es continua y derivable en un intervalo, entonces en algún punto dentro de ese intervalo la tasa de cambio instantánea de la función (la derivada) es igual a la tasa de cambio promedio de la función en ese intervalo.

Este teorema es de gran importancia en el cálculo diferencial, ya que nos permite establecer propiedades y características de las funciones a partir de su derivada. Además, es utilizado en la demostración de otros teoremas y en la resolución de problemas relacionados con la optimización y el análisis de funciones.

Explicación del Teorema del Valor Medio para Derivadas

El Teorema del Valor Medio es un concepto fundamental en el cálculo diferencial que establece una relación entre la derivada de una función y su incremento promedio en un intervalo dado. Este teorema establece que si una función es continua en un intervalo cerrado [a, b] y derivable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual al incremento promedio de la función en el intervalo [a, b].

En otras palabras, el Teorema del Valor Medio nos dice que si una función es continua y derivable en un intervalo, entonces en algún punto dentro de ese intervalo la tasa de cambio instantánea de la función (la derivada) es igual a la tasa de cambio promedio de la función en ese intervalo.

Ejemplos del Teorema del Valor Medio para Derivadas

El Teorema del Valor Medio para Derivadas es una herramienta fundamental en el cálculo diferencial que establece una relación entre la pendiente de una función en un intervalo y la tasa de cambio promedio en ese intervalo. Este teorema establece que si una función es continua en un intervalo cerrado [a, b] y derivable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual a la tasa de cambio promedio en el intervalo.

Por ejemplo, consideremos la función f(x) = x^2 en el intervalo [1, 3]. La derivada de esta función es f'(x) = 2x. Aplicando el Teorema del Valor Medio, sabemos que existe al menos un punto c en el intervalo (1, 3) donde la derivada de la función es igual a la tasa de cambio promedio en el intervalo. La tasa de cambio promedio en el intervalo es (f(3) – f(1))/(3 – 1) = (9 – 1)/2 = 4. Por lo tanto, existe al menos un punto c en el intervalo (1, 3) donde f'(c) = 2c = 4. Resolviendo esta ecuación, encontramos que c = 2.

Otro ejemplo es la función g(x) = sin(x) en el intervalo [0, π]. La derivada de esta función es g'(x) = cos(x). Aplicando el Teorema del Valor Medio, sabemos que existe al menos un punto c en el intervalo (0, π) donde la derivada de la función es igual a la tasa de cambio promedio en el intervalo. La tasa de cambio promedio en el intervalo es (g(π) – g(0))/(π – 0) = (0 – 0)/(π – 0) = 0. Por lo tanto, existe al menos un punto c en el intervalo (0, π) donde g'(c) = cos(c) = 0. Resolviendo

Teorema del Valor Medio para Integrales

El Teorema del Valor Medio es un concepto fundamental en el cálculo diferencial e integral. Este teorema establece que si una función es continua en un intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual al cociente de la diferencia de los valores de la función en los extremos del intervalo y la diferencia de los extremos del intervalo.

En términos más simples, el Teorema del Valor Medio nos dice que si una función es continua y diferenciable en un intervalo, entonces en algún punto dentro de ese intervalo la pendiente de la función será igual a la pendiente de la recta secante que une los puntos extremos del intervalo.

Este teorema es de gran importancia en el cálculo, ya que nos permite encontrar valores específicos de una función en un intervalo dado. Además, el Teorema del Valor Medio tiene diversas aplicaciones en diferentes áreas de la ciencia y la ingeniería, como la física, la economía y la estadística.

Explicación del Teorema del Valor Medio para Integrales

El Teorema del Valor Medio para Integrales es un concepto fundamental en el cálculo integral que establece una relación entre el valor promedio de una función en un intervalo y el valor de la función en algún punto dentro de ese intervalo. Este teorema es una extensión del Teorema del Valor Medio para Derivadas, que establece una relación similar pero para funciones derivables.

En términos más simples, el Teorema del Valor Medio para Integrales nos dice que si una función f(x) es continua en un intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la integral definida de f(x) en el intervalo [a, b] es igual al producto de la derivada de f(x) evaluada en c y la longitud del intervalo [a, b]. Matemáticamente, esto se expresa como:

∫_a^b f(x) dx = f(c) * (b – a)

Donde ∫_a^b f(x) dx representa la integral definida de f(x) en el intervalo [a, b], f(c) es el valor de la función en el punto c, y (b – a) es la longitud del intervalo [a, b].

Ejemplos del Teorema del Valor Medio para Integrales

El Teorema del Valor Medio para Integrales es una herramienta fundamental en el cálculo integral que establece una relación entre el valor promedio de una función en un intervalo y su derivada en algún punto dentro de ese intervalo. Este teorema es una extensión del Teorema del Valor Medio para Derivadas y nos permite obtener información sobre el comportamiento de una función en un intervalo dado.

Para comprender mejor este teorema, veamos algunos ejemplos. Supongamos que tenemos una función continua en el intervalo [a, b] y queremos encontrar el valor promedio de la función en ese intervalo. El Teorema del Valor Medio para Integrales nos dice que existe al menos un punto c en el intervalo (a, b) donde la función alcanza su valor promedio.

Por ejemplo, consideremos la función f(x) = x^2 en el intervalo [0, 2]. Para encontrar el valor promedio de esta función en ese intervalo, primero calculamos la integral definida de la función en ese intervalo, que es igual a (2^3)/3 – (0^3)/3 = 8/3. Luego, utilizamos el Teorema del Valor Medio para Integrales para afirmar que existe al menos un punto c en el intervalo (0, 2) donde la función alcanza su valor promedio de 8/3.

Este teorema también se puede aplicar a funciones que no son continuas en todo el intervalo, siempre y cuando sean continuas en el intervalo cerrado [a, b] y derivables en el intervalo abierto (a, b). En estos casos, el teorema nos asegura que existe al menos un punto c en el intervalo (a, b) donde la función alcanza su valor promedio.

En resumen, el Teorema del Valor Medio para Integrales nos proporciona una herramienta poderosa para analizar el comportamiento de una función en un intervalo dado. Nos permite encontrar el valor promedio de una función en un intervalo y establece una relación entre este valor promedio y la derivada de la función en algún punto dentro de ese intervalo.

Teorema del Valor Medio Generalizado

El Teorema del Valor Medio es un resultado fundamental en el cálculo diferencial que establece una relación entre la derivada de una función y su incremento promedio en un intervalo dado. Sin embargo, este teorema puede ser generalizado para funciones más generales que no necesariamente son diferenciables.

En su forma generalizada, el Teorema del Valor Medio establece que si una función f(x) es continua en un intervalo cerrado [a, b] y es diferenciable en el intervalo abierto (a, b), entonces existe al menos un punto c en el intervalo (a, b) donde la derivada de la función es igual al incremento promedio de la función en el intervalo cerrado [a, b]. Matemáticamente, esto se expresa como:

f'(c) = \frac{f(b) – f(a)}{b – a}

Este teorema es de gran importancia en el análisis matemático, ya que proporciona una herramienta fundamental para el estudio de las propiedades de las funciones y la resolución de problemas relacionados con ellas. Además, el Teorema del Valor Medio tiene diversas aplicaciones en diferentes áreas de la ciencia y la ingeniería, como la física, la economía y la estadística.